Los eventos se pueden componer por medio de la unión o la intersección de dos o mas eventos.
La unión se denota por (U), sean los eventos A, B, la unión de estos dos eventos esta compuesta por todos los puntos muestrales que pertenecen a A, a B o ambos eventos, sin repetir puntos muestrales.
La intersección se denota por ( ), sean los eventos A, B, la intersección de estos dos eventos esta compuesta por los puntos muestrales que son comunes a A y a B.
Nota: La variable que representa el número de puntos muestrales favorables para cada evento compuesto, es decir los eventos simples que componen el evento, se representa por la letra m, tanto para la unión como para la intersección, con el fin de poder generalizar con una sola notación los casos favorables al evento compuesto resultante.
Caso especial en la intersección de dos eventos, si el evento A esta contenido en el evento B,
Eventos Mutuamente Excluyentes: También se conocen como eventos disyuntos y son aquellos eventos que perteneciendo a un mismo espacio muestral no tienen puntos muestrales en común, es decir son eventos que no pueden suceder al mismo tiempo o que no comparten puntos muestrales, sean los eventos A, B, la intersección de estos dos eventos en el conjunto vació.
Eventos Complementarios: Dos eventos son complementarios si y solo si son disyuntos y la unión de ellos conforma el espacio muestral, sea el evento A, el complemento de A se denota por A, entonces el evento A esta compuesto por todos los puntos muestrales que le faltan a A para ser igual al espacio muestral.
Eventos Colectivamente Exhaustivos: Dos o mas eventos son colectivamente exhaustivos si y solo si la unión de ellos conforman el espacio muestral, es decir dos eventos complementarios son colectivamente exhaustivos, pero dos eventos colectivamente exhaustivos no siempre son complementarios,
Ejemplo 2
La probabilidad del número de helados vendidos por día en la heladería Copo de Nieve se presente en la siguiente tabla:
Sean los siguientes eventos:
A: Vender menos de 24 helados en un día.
B: Vender 22 helados o mas en un día.
C: Vender entre 21 y 25 helados en un día.
D: Vender mas de 26 helados en un día.
Con esta información calcular la probabilidad de los siguientes eventos compuestos:
Solución:
El espacio muestral es
A cada punto muestral se la asignara su respectivo evento simple como aparece en la tabla
Los eventos A, B, C, D están compuestos por los puntos muestrales:
Respectivamente.
Como los puntos muestrales no son equiprobables es necesario mostrar la composición de los eventos de acuerdo a los eventos simples que les corresponden, así:
Respectivamente
Donde m = 8, porque la unión entre B y C esta compuesta por 8 eventos simples
Por lo tanto
Entonces
Donde m = 8, porque la unión entre A, C y D esta compuesta por 8 eventos simples
Por lo tanto
Entonces
Nótese que el valor que toma m es igual para la solución del punto a y b, pero no involucra los mismos puntos muestrales o eventos simples.
Donde m = 0, porque la intersección entre A y D no tiene eventos simples comunes
Por lo tanto
como la
Donde m = 2, porque la intersección entre A, B y C esta compuesta por 2 eventos simples
Por lo tanto
Entonces
Caso especial en la intersección de dos eventos, si el evento A esta contenido en el evento B,
P(AB) = 0, en general P ( ABCD...) = 0
Eventos Complementarios: Dos eventos son complementarios si y solo si son disyuntos y la unión de ellos conforma el espacio muestral, sea el evento A, el complemento de A se denota por A, entonces el evento A esta compuesto por todos los puntos muestrales que le faltan a A para ser igual al espacio muestral.
Eventos Colectivamente Exhaustivos: Dos o mas eventos son colectivamente exhaustivos si y solo si la unión de ellos conforman el espacio muestral, es decir dos eventos complementarios son colectivamente exhaustivos, pero dos eventos colectivamente exhaustivos no siempre son complementarios,




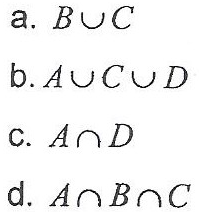














No hay comentarios:
Publicar un comentario